はじめに

実際の建物を立てるとその建物は、必ず沈下してしまします。これはどんなに気をつけていても避けられないものです。ではこのとき実際にどれくらい沈下しそうなのかを予測することが大事になってきます。

今回はその沈下予測の方法として、即時沈下と圧密沈下の2つに分けて紹介します。どちらも今回の計算方法は1次元での計算であることを念頭に置いてこの先お読みください。

沈下とは

現実の建物はいわゆる地盤、土の上に立っています。つまり、建物の重さを土が支えているのです。このとき土に思いっきり力を加えると大きさが変化することが思い起こされます。現実でも同様のことが起こっているのです。

地盤の上にものを置くと必ず沈下するというのはパッと聞いただけでは誤りのように感じます。しかし、ソファーに腰掛けるとスプリングが沈み込むように、必ず起きうる問題なのです。

このとき実際の沈下は大きく分けて2種類に分けられることが知られています。即時沈下と圧密沈下です。この2種の違いを定性的な面から見てみましょう。

即時沈下

即時沈下とは、その名の通り建物が建て終わったら速やかに起こる沈下のことです。数時間から数分で沈下が完了するのが特徴です。

メカニズムとしては、バネを想像するのがもっとも良いでしょう。バネは力を加えると速やかに伸び縮みします。同様に土でも同じような反応が見られるのです。しかし、注意点があります。これは完全に弾性的な変形ではないからです。土の変形は殆どの場合塑性的です。なぜならば、土は押しつぶすと土粒子の配列が変化し、より密な構造になります。このように不可逆な変化を含んでいるのです。

もっと大きな違いを述べるならば、即時沈下の最中は水の出入りはありません。水の出入りは時間がかかる現象でしたから当然といえば当然です。

圧密沈下

圧密沈下は、建物が建て終わったあと時間をかけて起こる沈下のことです。数年かけて沈下し続けるのが特徴的です。その名の通り、圧密による土の体積変化と深い関係があります。つまり、排水を伴うということです。正確に計算するならば圧密方程式を解いてあげなければいけません。とはいえ、多くの場合は圧縮曲線を用いて圧密沈下量を予測することがほとんどです。ここから、載荷重量に対して反応は徐々に鈍っていくことがわかります。

沈下量計算

前節で沈下の様態が二種類に大別できることを述べました。実際に沈下の様子を計算するわけですがここで大きな問題があります。実際の地盤はとても複雑であるということです。今回の計算はいわゆる一次元圧密と呼ばれる方法で計算してみることにします。これは最もシンプルで、電卓で簡単に計算できるという点が特徴です。四則演算とグラフの読み取りだけで計算できるという点は優秀ですが、かなり安全側に見た(過大に沈下量を評価した)手法でもあるため、あくまで目安として使われる方法になります。

一次元圧密の仮定

一次元圧密は計算を簡単にするために多くの(非現実的な)仮定が含まれています。

• 応力伝達は1次元的である。
  • ポアソン比がゼロ
• 沈下量計算は、安定地盤と地表面のちょうど中点を代表にとって計算する。
  • 応力分布を計算しない。

計算の仮定は重要ですからきちんと理解しておきましょう。

即時沈下量

即時沈下量は定性的な点で話したようにバネの縮みのつもりで計算します。基本的には以下の式になります。ただし即時沈下量を$S_f$[m]、その地盤をバネとみなしたときの弾性係数$E$[kN/m²]、安定地盤までの深さをH[m]、建物が地盤に与える応力を$q$[kN]とします。

$$S_f=\frac{q}{E}H$$

このとき弾性係数$E$[kN/m²]は多くの場合一軸圧縮試験から得られる土の変形係数$E_{50}$[kN/m²]を用いることが多いです。

もしくは正方形基礎だと思いこむことで即時沈下量を計算するケースもあります。これは以下の式になります。ただし、基礎の面積ををA[m]とします。

$$S_f=\frac{0.6Q}{E\sqrt{A}}$$

この式は以下で示す二次元応力伝達を考えたときの式から計算できます。ポアソン比が0と仮定していることに注意して変形すると同型の式が得られます。

インターネットで即時沈下量について調べると、様々な種類の式が出てきます。これは、ブシネスクの応力分布を適用させたり、きちんと弾性理論を解いた場合の式になります。これらは今回よりもより現実に近い仮定を行うことでより精度の高い計算ができるようになります。詳細はここでは、述べませんがいわゆる二次元応力伝達を考えたときの即時沈下量を示します。ただし、基礎幅をB[m]、土のポアソン比を$\nu$、影響係数を$I_\rho$とします。

$$S_f=qB\frac{1-\nu^2}{E}I_\rho$$

影響係数$I_\rho$は形や奥行きの長さなど多くの要素から決定される補正項です。精度良く計算するために多くの検討が必要であるため利用する際は注意してください。正方形基礎であれば影響係数は0.6程になります。

圧密沈下量

圧密沈下量は圧密によって発生する沈下量です。今回は最後まで圧密が完了したときの沈下量計算について述べます。初期圧密圧力は載荷前の中点の載荷荷重の変化量からひずみを計算し、全体にかけあわせて沈下量を計算します。計算方法はいくつかありますが今回は圧縮曲線法で説明をします。式は以下の通りになります。ただし、圧密沈下量を$S_c$[m]、載荷前の間隙比を$e_b$、載荷後の間隙比を$e_a$、地盤の厚さをH[m]とします。

$$S_c=\frac{e_b-e_a}{1+e_b}H$$

これをより詳細に計算するには以下のような補正があります。細かい層ごとに分けてそれぞれ計算する。他には、ポアソン比により実際には応力が減少していることを考慮する。つまり、応力球根を活用することがあります。これらの計算は体積積分が必要になりますのでここでは触れないことにします。

圧密沈下の時間変化

圧密沈下は非常に長い時間がかかると述べました。そのため、最終圧密のときの沈下量を示したわけです。現実的には完了していることは稀です。圧密過程における圧密沈下について少し述べておくことにします。

圧密沈下過程では排水を伴うのでした。これは、水圧が高いため外に逃げ出すことを意味しています。逆に言えば水圧だけ、土の圧力は低下しています。この時、土の圧力と間隙比にはある関係があります。これを圧密圧力−間隙比曲線(e-logp曲線)と呼びます。これによって現在の間隙比を計算できます。そのため、今の水圧と土の圧力が分かれば、今現在の沈下量を計算できることになります。正確に計算したい場合、圧密方程式を解くことで得られます。今回は簡便にできる理論圧密曲線法を用いることにします。

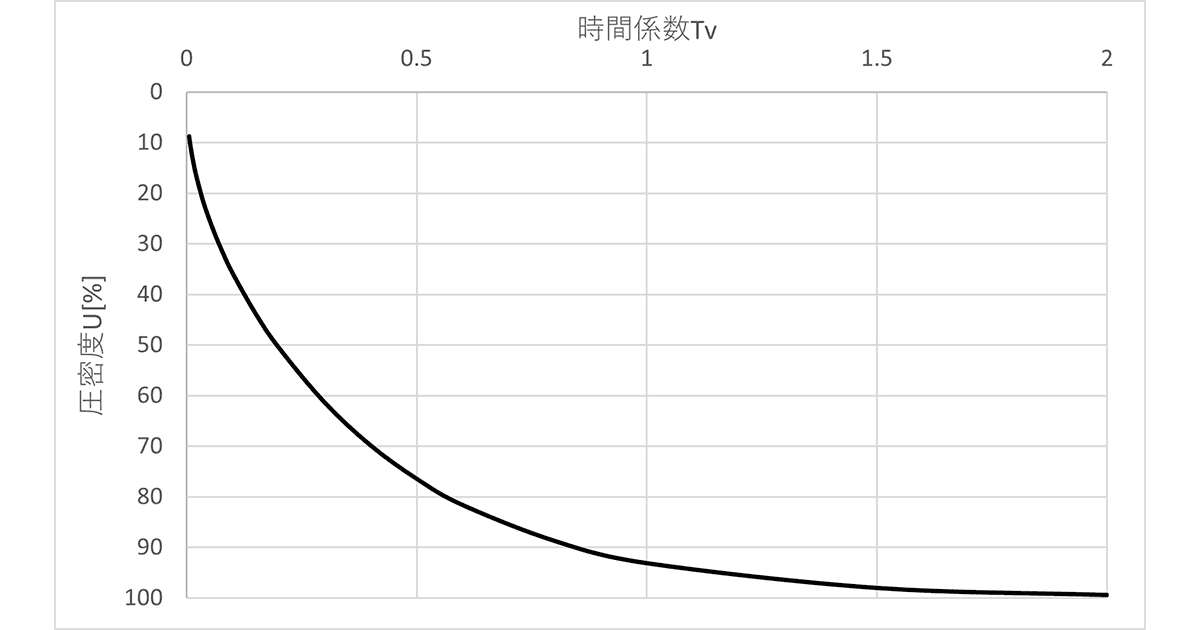
圧密曲線法は圧密の進行度合いを、時間、沈下量の比率で計算するものです。これは圧密方程式の理論解をいろんなものに対応できるようにしたものです。

この時、時間を時間係数$Tv$に沈下量を圧密度$U$[%]とおきます。また、圧密係数$cv$、圧密を受けている層の厚さを$H$ m、時刻$t$ での沈下量を $s$ mと置きます。

$$Tv=\frac{cv}{\left(\frac{H}{2}\right)^2}t$$

$$U=100\frac{s}{S_c}$$

これが下図に適合することを用いて現在の沈下量を計算します。

最後に

今回は即時沈下と圧密沈下における沈下量計算について概説しました。沈下予測は設計においた重要な観点です。