はじめに

土は最も安価で、ありふれた材料です。それだけでなく、地上に建物を立てるときにはいつも、お世話になります。そのため、土の強度を知ることは建物の安定性を把握したり、材料として使うときにとても重要になります。

今回は土の強度に関わる物理量を見ていきましょう。そののち、土の強度を評価する、クーロンの破壊基準、モールクーロンの破壊基準についてそれぞれ見ていきましょう。

土の構成

土はつぶつぶの土粒子と、水、そして空気から構成されていると考える三相モデルで考えることが多いです。強度もまた同じように考えることになります。

この図は土を模した図です。丸いのが土で、水色なのが水と空気だと思ってください。このとき上から押しつぶすと土の粒子はそれぞれずれようとします。すなわち、土はいつでもせん断力によって破壊しようとするわけです。これからせん断力の計算について考えていくことにします。

せん断力と摩擦の類似性

ところで、ずれると聞いたときに最も思い起こされるのは摩擦ではないでしょうか。摩擦力は面に押し付ける力の定数倍だけ働くのでした。土粒子はたしかに細かく見ると、それぞれ別の方向に垂直効力とせん断力を受けています。このときすごく離れた目で見ると、土砂崩れのようにある角度で壊れることが容易に想像できます。このようにマクロな視点から考えていけば、せん断力がわかりやすくなるでしょう。

このとき、マクロな視点で見たとき、土を取り扱うのはちょっと面倒です。なぜなら、マクロな視点で見ると土は連続的にできた物質になるからです。これらを全部まとめて取り扱うのは難しいため、土から切り出してきた一部分だけで考えることにしましょう。すなわち、力を一括で扱うのではなく、単位面積に掛かる力、すなわち圧力に分けて考えるということです。

有効応力と間隙水圧

マクロに見ると意気込んだところですが大きな問題があります、土は土粒子だけでなく、水を含んでいるのでした。これは土に加えた圧力がすべて土粒子に伝わるわけではないことを意味しています。土に加えられた圧力は土粒子と水の2つが負担しているのです。これではややこしいので用語を定義することにしましょう。ちなみにですが、圧力のことを材料系の学問では応力と呼ぶことがあります。材料力学で扱うものはすべて連続体だからです。

全応力

全応力はこの土が受けているすべての圧力のことです。静止状態であれば、力の釣り合いから簡単に求めることができます。一般には $\sigma$ と書きます。

有効応力

有効応力は全応力の中で、実際に土が支えている圧力のことを意味します。水と異なり簡単にいなくなったりはしないため実際に土で有効的に支えている強度という意味で使われます。一般には $\sigma '$ と書きます。

間隙水圧

間隙水圧は隙間に入った水が支えている圧力のことを意味しています。ベルヌーイの定理という水理学(流体力学)の式を用いて計算します。最大の特徴として水は気軽に出入りするため、間隙水圧を高めると水が逃げていってしまします。このことから地盤の間隙水圧を測ることで水の出入りについて調べることができます。一般には $u$ と書きます。

実際のところ水の出入りが無い、状態であればベルヌーイの定理から水の密度 $ρ_w$、自分より上にある水の量 $h$ (単位体積あたりですので実質的には高さ)、重力加速度 $g$ から計算することもできます。いわゆる $ρ_wgh$ と呼ばれるあれです。

このとき、いつでも以下の式が成立するのは説明的にも明らかですね。

$$\sigma=\sigma ' +u$$

感覚的にこの式を説明するならば、外から加えられた力は、土と水が協力して対抗するということです。このとき水は簡単に逃げるわけですから土の強度はこの有効応力だけで考えていくことになります。このとき有効応力はある直線方向の力であり滑りの力ではない、すなわち垂直抗力部分であることに気をつけてください。

モールの応力円

土の強度は有効応力で考えるという話が前までの話でした。このとき垂直の力と滑りの力の方向を考えて上げる必要があります。では、土の滑る方向はどっちなのか皆目検討が付きません。このとき垂直の力と横滑りする力の組を考えるモールの応力円を使って考えて行きます。

力の釣り合いは、いつでも成立するはずです。なら、傾けたとしても力はいつでも釣り合うはずです。このときすべての方向の力の釣り合いから求めたせん断力と垂直応力の組を図にプロットすると円になります。この円をモールの応力円とよんでいます。

この図がいわゆるモールの円です。一つの円がある状態の土を表現しているということになります。このとき横軸の $\sigma '$ が面に垂直な力を意味しています。縦軸の $\tau '$ は横滑りの力のせん断力になります。ついでに、この円から、せん断力が0であるときに有効応力が最大、最小になることがわかります。このときの面を主応力面とよび大きい方を $\sigma_1 '$、小さい方を $\sigma_3 '$ と書きます。このとき2がないのは、本来は奥行方向にも回転可能であるからです。奥行方向に適切に回転させるとまたまた主応力があります。

これまでの話で、土内部の現在の力の様子がわかるようになりました。あとはどのタイミングで壊れるのかを考えていきましょう。

クーロンの破壊基準

これを考える上で、ある応力面で壊れたと考えてみましょう。

このとき摩擦のアナロジーから応力に従う摩擦力が働きます。このことを角度$\phi '$をつかって

$$\sigma '\tan \phi '$$

と書いてみます。このとき摩擦係数を角度で書いたのには理由があります。摩擦係数は重力下において滑り始めたときの斜面角度のタンジェントでかけることが知られています。土が滑り始めるのもだいたい重力のせいなのでタンジェントで書くことにしたのです。このとき角度 $\phi '$ をせん断抵抗角もしくは内部摩擦角と呼びます。

他にも土同士が引き合う力を考えてあげる必要があります。この力の存在は泥団子を作ってみるとよく分かるでしょう。泥団子を作るときれいに丸く作ることができます。このとき地面についていない部分は、重力と上から引き上げられる力で釣り合っているはずです。このように粒子間をくっつける力、粘着力があります。これを $c'$ と書くことにします。

壊れた瞬間は働いているせん断力とこれに抵抗する力は等しくなるはずです。このことから以下の等式が成立します。

$$\tau '=c'+\sigma '\tan \phi '$$

この式のことをクーロンの破壊基準と呼んでいます。この式は実験式ではあるものの、広い範囲で適用可能な式として知られています。このときの $c'$ と $\phi '$ を実験で調べることで、実際の土の強度を予想できるようになるのです。

この式は壊れたときにモール円に接しているはずなので別な見方をすると、包絡線になります。実際の実験でも複数回実験し最も最適な包絡線を考えることが多くあります。

とは言え、不飽和土ではきれいな直線にならない場合もあるので注意が必要です。

モールクーロンの破壊基準

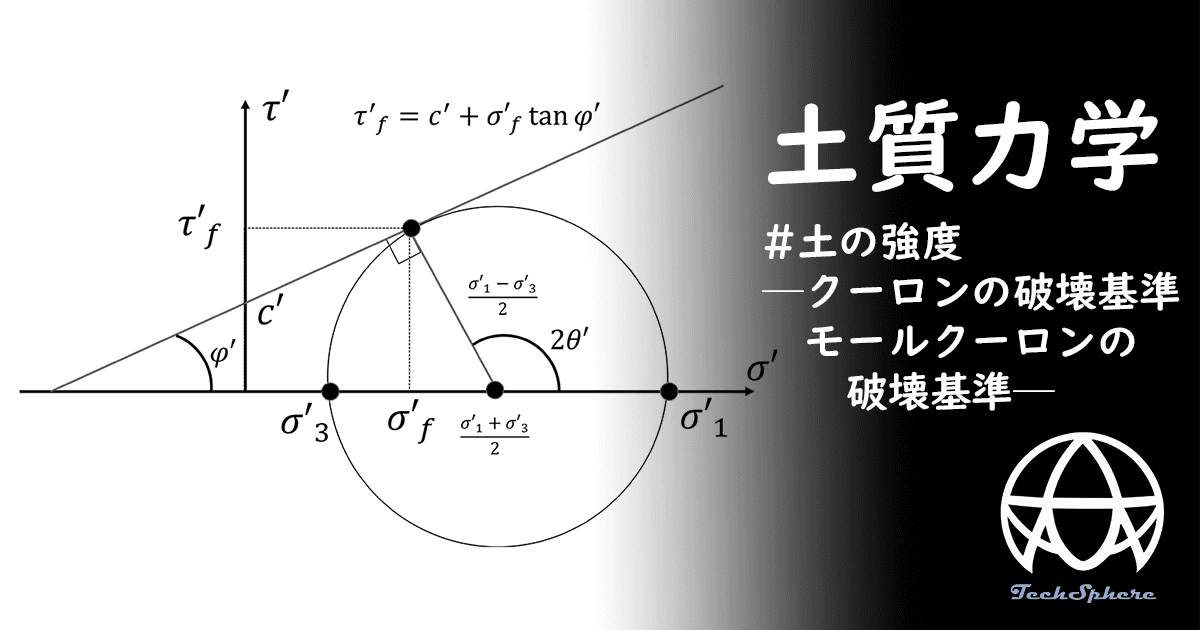
クーロンの破壊基準とモール円を組み合わせて主応力だけで表現してみましょう。このとき図は以下になります。

モールの円は主応力 $\sigma_1 '$ 、$\sigma_3 '$ を半径にする円でした。これはクーロンの破壊基準と一点で接しています。このときの応力とせん断力を $\sigma_f '$、$\tau_1 '$ と書いておきましょう。また円の半径は $\frac{\sigma '_1-\sigma ' _3}{2}$、円の中心座標は $\frac{\sigma '_1+\sigma ' _3}{2}$ になります。

次にクーロンの破壊基準を考えます。$\tau '$ は切片が $c'$ で傾きが $\tan \phi'$ の直線です。このとき、主応力でクーロンの破壊基準を表現してみましょう。クーロンの破壊基準の式と$\sigma '$軸の交点から、モールの応力円までの距離を考えると以下になります。

$$\frac{c'}{\tan \phi'}+\frac{\sigma '_1+\sigma ' _3}{2}$$

このとき図に書いた直角のマークがある三角形のサインを考えると以下になります。

$$\begin{aligned}\sin \phi'=\frac{\frac{\sigma '_1-\sigma '_3}{2}}{\frac{c'}{\tan \phi'}+\frac{\sigma '_1+\sigma '_3}{2}}\\\frac{\sigma '_1-\sigma '_3}{2}=\left(\frac{c'}{\tan \phi'}+\frac{\sigma '_1+\sigma '_3}{2}\right)\sin \phi'\\\frac{\sigma '_1-\sigma '_3}{2}=c'\cos \phi ' +\frac{\sigma '_1+\sigma '_3}{2} \sin \phi'\end{aligned}$$

この式をモールクーロンの破壊基準と呼びます。じっさいの試験では多くの場合主応力を計測するのでこちらのほうが使い勝手が良いです。

まとめ

今回は、土の強度を評価する方法について述べていきました。土は身近で、すべての建物の下にあるため強度は重要になります。他の材料と異なり特殊な式で評価しているのが特徴だと覚えておきましょう。